Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện thông qua thể tích khối tứ diện vuông
Chọn B
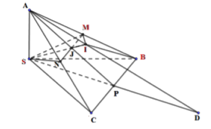
Do nên các tam giác vuông tại
đôi một vuông góc.
Thể tích khối tứ diện vuông là:
Gọi là giao điểm của và , là giao điểm của và . Khi đó,
(do )
có: là trung điểm của , là trung điểm của
Xét tam giác vuông có
Ta có: .
Áp dụng định lí Menelaus trong tam giác ta có:
Áp dụng định lí Cosin trong tam giác ta có:
Dễ dàng chứng minh được: hay
Lại có:
.

